Quick sort
Quick sort 的精神在于将大区间分割为小区间,分段排序。每个小区间排序完成后,串接起来的大区间就完成了排序。最坏的情况发生在分割时产生出的一个空的子区间。
threshold(阈值)
面对一个只有十来个元素的小序列,使用像 Quick sort 这样复杂而(可能)需要大量运算的排序算法,是否划算?
在小数据量的情况下,甚至简单如 Insertion Sort 者也可能快过 Quick Sort ——因为 Quick Sort 会为了极小的子序列而产生许多的函数递归调用。监狱这种情况,适度的评估序列的大小然后决定采用 Quick Sort 或者 Insertion Sort 是值得采纳的一种优化措施
introsort
不适当的枢轴选择,导致不当的分割,导致 Quick Sort 恶化为 O(N^2) 。混合式排序算法 Introspective Sorting( 内省式排序 ), 简称 IntroSort ,其行为在绝大部分情况下几乎与 median-of-3 Quick Sort 完全相同。但是当分割行为 (partitioning) 有恶化为二次行为的倾向时,能够自我侦测,转而改用 Heap Sort 。使其效率维持在 Heap Sort 的 O(N*logN), 又比一开始就用 Heap Sort 来得好。
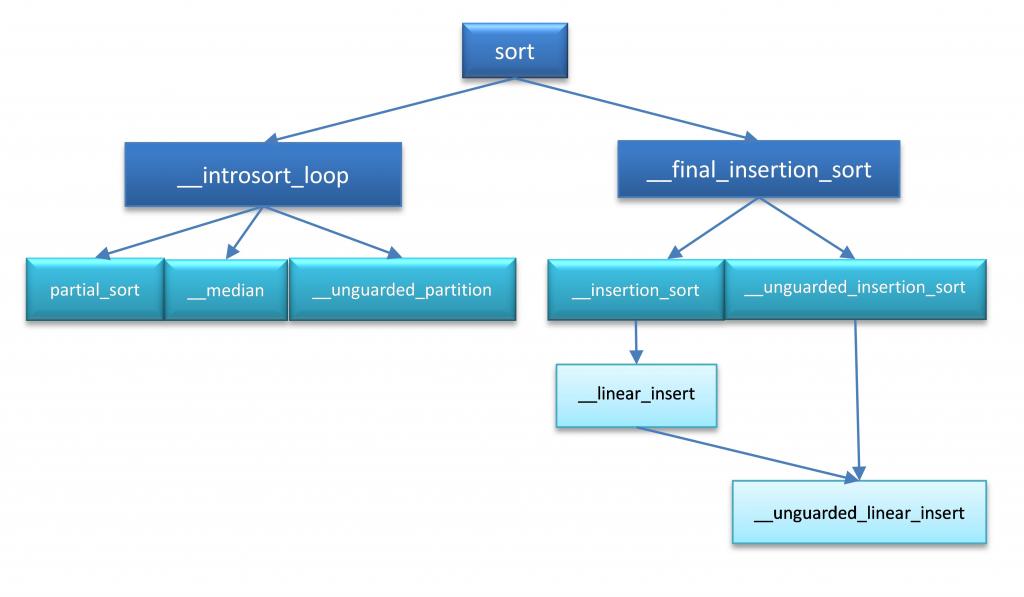
SGI STL Sort 函数依赖关系
SGI STL Sort 源码
const int __stl_threhold=16; // 阈值,用于评估序列大小
// 千万注意: sort() 只适用于 RandomAccessIterator
template <class RandomAccessIterator>
inline void sort (RandomAccessIterator first, RandomAccessIterator last) {
if (first != last) {
__introsort_loop (first, last, value_type(first), __lg (last - first) * 2);
__final_insertion_sort (first, last);
}
}
//__lg() 用来控制分割恶化的情况。
// 找出 2^k <= n 的最大值 k 。例, n=7 ,得 k=2 , n=20 ,得 k=4 , n=8 ,得 k=3 。
template <class Size>
inline Size __lg (Size n) {
Size k;
for (k = 0; n > 1; n >>= 1) ++k;
return k;
}
// 完成后将返回母函数 sort() 在进入 __final_insertion_sort() 最终完成排序
template <class RandomAccessIterator, class T, class Size>
void __introsort_loop (RandomAccessIterator first,
RandomAccessIterator last, T*,
Size depth_limit) {
// 以下, __stl_threshold 是个全局常数,稍早定义为 const int 16 。
// 判断序列大小,如果小于等于 16 使用 Quick Sort 的排序,留给 Insertion Sort 最终完成排序
while (last - first > __stl_threshold ) {
if (depth_limit == 0) { // 至此,切割恶化,改用 heapsort
partial_sort (first, last, last); // partial_sort 是以 Heap Sort 实现
return;
}
--depth_limit;
// 以下是 median-of-three partition ,选择一个够好的枢轴并决定切割点。
// 切割点将落在迭代器 cut 身上。
RandomAccessIterator cut = __unguarded_partition
(first, last, T( __median (*first, *(first + (last - first)/2),
*(last - 1))));
// 对右半段递归进行 sort.
__introsort_loop (cut, last, value_type(first), depth_limit);
last = cut;
// 现在回到 while 循环,准备对左半段递归进行 sort.
// 这种写法可读性较差,效率并没有比较好。
}
}
// 以插入排序完成最后的排序
template <class RandomAccessIterator>
void __final_insertion_sort (RandomAccessIterator first,
RandomAccessIterator last) {
if (last - first > __stl_threshold ) {
// 分为两段前者调用插入排序,因为后段的元素总是比前段大(由 Quick Sort 性质可知),所以先
// 调用前者完成前段排序,然后将后段从尾部遍历的方式插入已序的元素中
__insertion_sort (first, first + __stl_threshold);
__unguarded_insertion_sort (first + __stl_threshold, last);
}
else
__insertion_sort (first, last);
}
template <class RandomAccessIterator>
inline void __unguarded_insertion_sort (RandomAccessIterator first,
RandomAccessIterator last) {
__unguarded_insertion_sort_aux (first, last, value_type(first));
}
template <class RandomAccessIterator, class T, class Compare>
void __unguarded_insertion_sort_aux (RandomAccessIterator first,
RandomAccessIterator last,
T*, Compare comp) {
for (RandomAccessIterator i = first; i != last; ++i)
__unguarded_linear_insert(i, T(*i), comp);
}
// 对指定区域完成插入排序
template <class RandomAccessIterator>
void __insertion_sort (RandomAccessIterator first, RandomAccessIterator last) {
if (first == last) return;
for (RandomAccessIterator i = first + 1; i != last; ++i) // 外循环
__linear_insert (first, i, value_type(first)); // first,i 形成一个子范围
}
template <class RandomAccessIterator, class T>
inline void __linear_insert (RandomAccessIterator first,
RandomAccessIterator last, T*) {
T value = *last; // 记录尾元素
if (value < *first) { // 尾比头还小(那就别一个个比较了,一次做完…)
copy_backward (first, last, last + 1); // 将整个范围向右递移一个位置
*first = value; // 令头元素等于原先的尾元素值
}
else
__unguarded_linear_insert (last, value);
}
// 由末尾遍历,将数据插入到已序元素中去。
template <class RandomAccessIterator, class T>
void __unguarded_linear_insert (RandomAccessIterator last, T value) {
RandomAccessIterator next = last;
--next;
while (value < *next) {
*last = *next;
last = next;
--next;
}
*last = value;
}
// 传回 a,b,c 之居中者
template <class T>
inline const T& __median (const T& a, const T& b, const T& c) {
if (a < b)
if (b < c) // a < b < c
return b;
else if (a < c) // a < b, b >= c, a < c
return c;
else
return a;
else if (a < c) // c > a >= b
return a;
else if (b < c) // a >= b, a >= c, b < c
return c;
else
return b;
}
template <class RandomAccessIterator, class T>
RandomAccessIterator __unguarded_partition (RandomAccessIterator first,
RandomAccessIterator last,
T pivot) {
while (true) {
while (*first < pivot) ++first; // first 找到 >= pivot 的元素,就停下来
--last; // 调整
while (pivot < *last) --last; // last 找到 <= pivot 的元素,就停下来
// 注意,以下 first < last 判断动作,只适用于 random iterator
if (!(first < last)) return first; // 交错,结束循环。
iter_swap (first, last); // 大小值交换
++first; // 调整
}
}本文作者 : cyningsun
本文地址 : https://www.cyningsun.com/04-09-2011/stl-introsort.html
版权声明 :本博客所有文章除特别声明外,均采用 CC BY-NC-ND 3.0 CN 许可协议。转载请注明出处!
