B+树 —— 数据库的灵魂

1. 背景
2. B+ 树
   1. 定义
   2. 算法
      1. 查找
      2. 插入
      3. 删除
3. 复合索引
4. 聚簇索引
5. 总结

背景

虽然 Nosql 风生水起，关系型数据库在当前的开发中仍然扮演着不可或缺的角色。因此在面试中也会被时常问到，很多问题即使是工作多年的同学仍然会磨棱两可，例如：

1. 为什么使用B+树，而不是B树作为底层数据结构？
2. 最左前缀匹配原则 为什么跟索引中字段顺序相关，而与查询中字段顺序无关？
3. Like 查询能够使用索引吗？
4. 主键为什么最好选择递增的字段？

很多人把原因归结于没有认真准备。靠记忆死记硬背终归落了下乘，归根结底还是没有把握住本质。MySQL的本质是什么？当然是其存储引擎。要想对数据库有本质的认识，了解存储引擎底层的数据结构 B+树 是一堂必修课。

B+ 树

定义

如果此B+树的阶数是 m+1，则：

• 每个节点最多有 m 个 Key 及 m+1 个子节点
• 除根节点外，所有节点必须半满（Half-full）
• 如果 m 是 偶数，且 m = 2d
  • 叶节点半满：至少有 d 个Key
  • 非叶节点半满：至少有 d 个Key
• 如果 m 是奇数，且 m = 2d+1
  • 叶节点半满：至少有 d+1 个 Key
  • 非叶节点半满：至少有 d 个Key

算法

查找

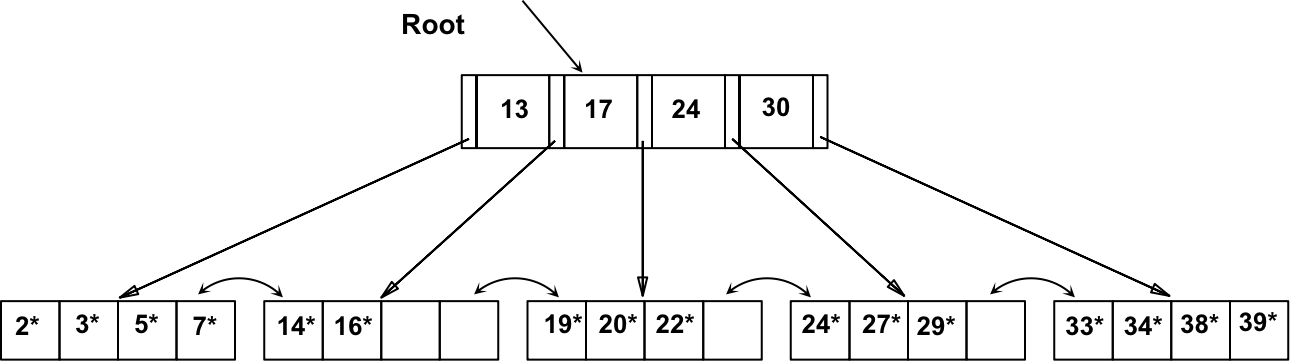
从根节点开始，检查非叶子节点的索引项，可以使用二分（或线性）搜索进行查找，以找到对应的子节点。沿着树向下遍历，直到到达叶节点

根据以上方法查找 15*，可知它不在该树上

插入

1. 首先，查找要插入的 叶节点 L

2. 接着把数据项插入这个节点中

   • 如果没有节点处于违规状态，则处理结束
   • 否则，均匀的拆分 L 为两个节点（ L和 新节点 L2），使得每个都有最小数目的元素
     • 将索引项中间的 key 复制到父节点（Copy up）
     • 将指向 L2 的索引项插入到 L 的父节点

3. 沿树递归向上，继续这个处理直到到达根节点

   • 若要拆分索引节点，需均匀地拆分索引条目，将中间的 key 移动到父节点（Push up）

     与叶节点拆分对比操作不同

4. 如果根节点被分裂，则创建一个新根节点。

假设，将 8* 插入到上述 B+ 树，观察在叶节点和非叶节点拆分中如何保证半满的。并注意 Copy up 和 Push up 之间的区别，确保理解其中的原因。

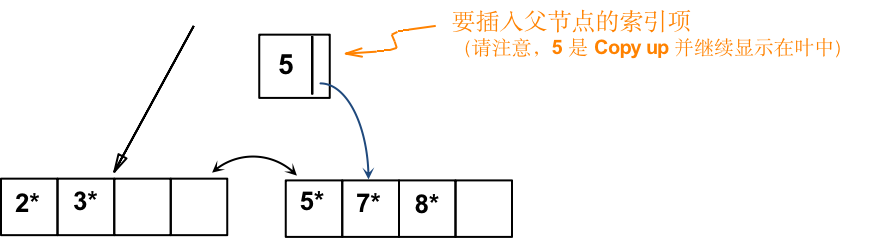
a) 首先找到的 叶节点 L，并拆分

• 将 索引项的 key 5 Copy up
• 将 指向 L2 的 索引项指针添加到 L 的 父节点

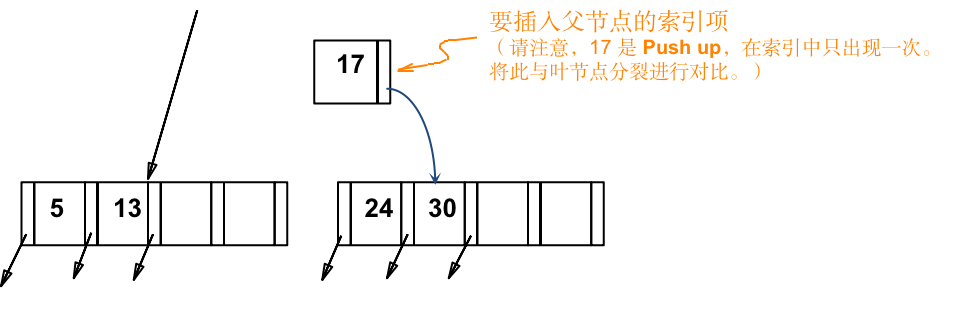
b) key 5 Copy up 到父节点子后，导致非叶节点拆分：

• 17 Push up 到 父节点

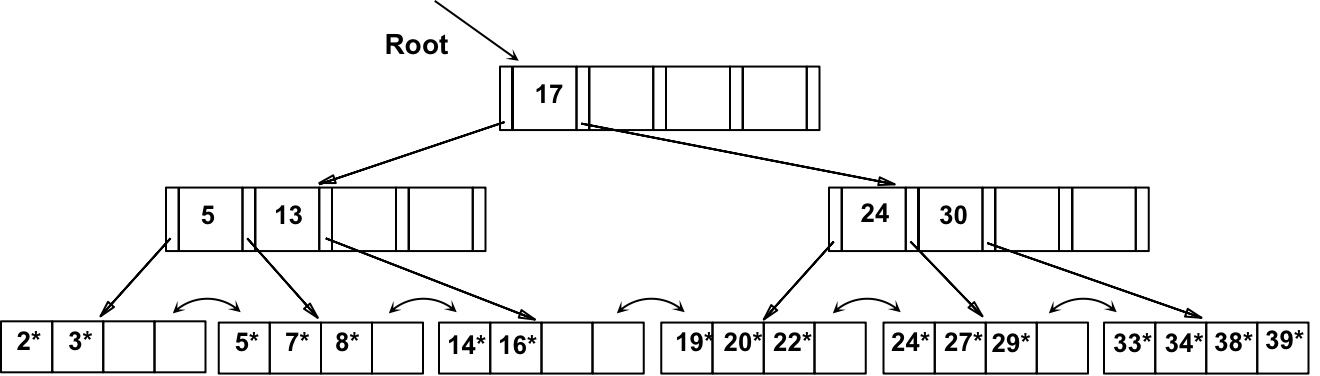
c）最终根节点被拆分，并导致树高度增加，得到以下B+树

删除

1. 从根节点开始，查找该项归属的 叶节点 L
2. 删除该项
   • 如果叶节点L 多于半满，则处理结束
   • 如果叶节点L 不足半满的索引项
     • 尝试从兄弟节点（与L具有相同父级的相邻节点）借索引项，重新分配。
     • 如果重新分配失败，则合并 L 和 兄弟节点
3. 如果发生合并，则必须从L的父索引项中删除索引项（指向L或兄弟节点的）
4. 递归此处理直到节点是合法状态，或者到达根节点。

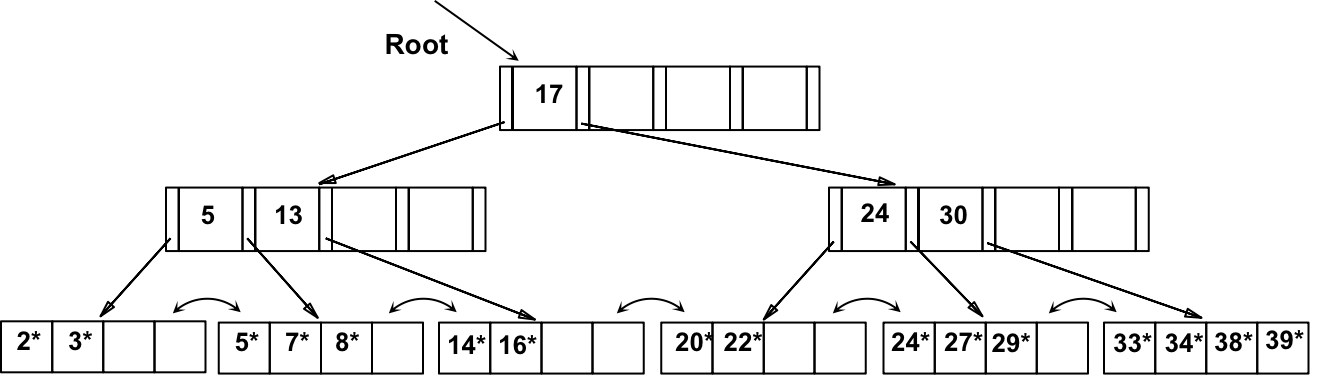
假设，对上述B+树，依次删除 19*、20*、24*

a) 删除 19*，较为简单，得到

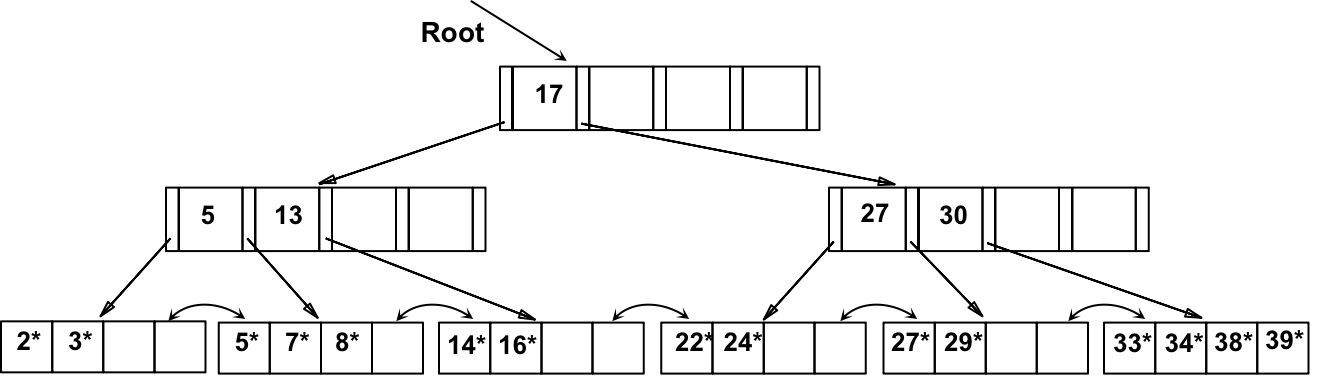
b) 删除 20*，是通过重新分配完成的。注意中间的 key 是如何 Copy up 的

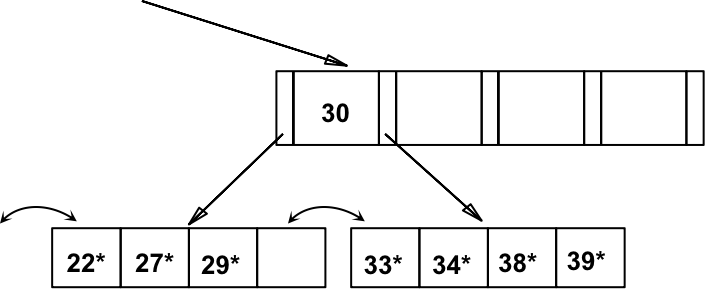
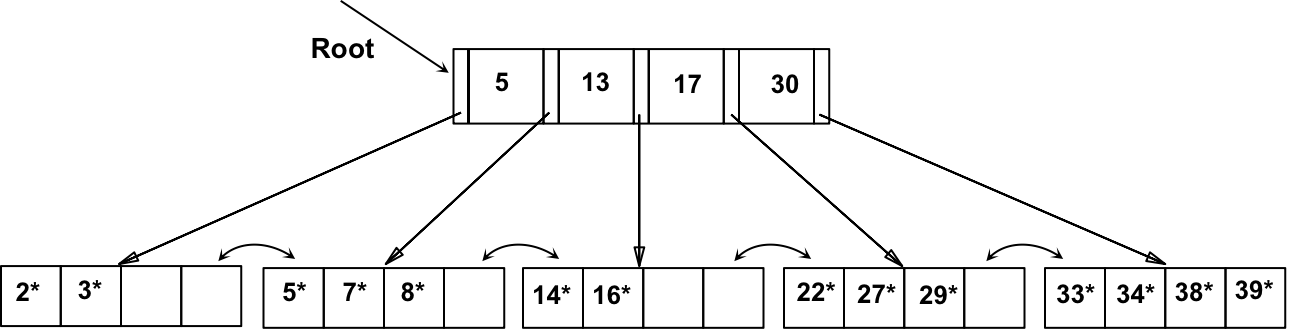
c) 删除 24*，导致与右侧索引项的合并。

然后，沿树向上，父节点同样需要与左侧兄弟节点合并，导致根节点的 “pull down”

复合索引

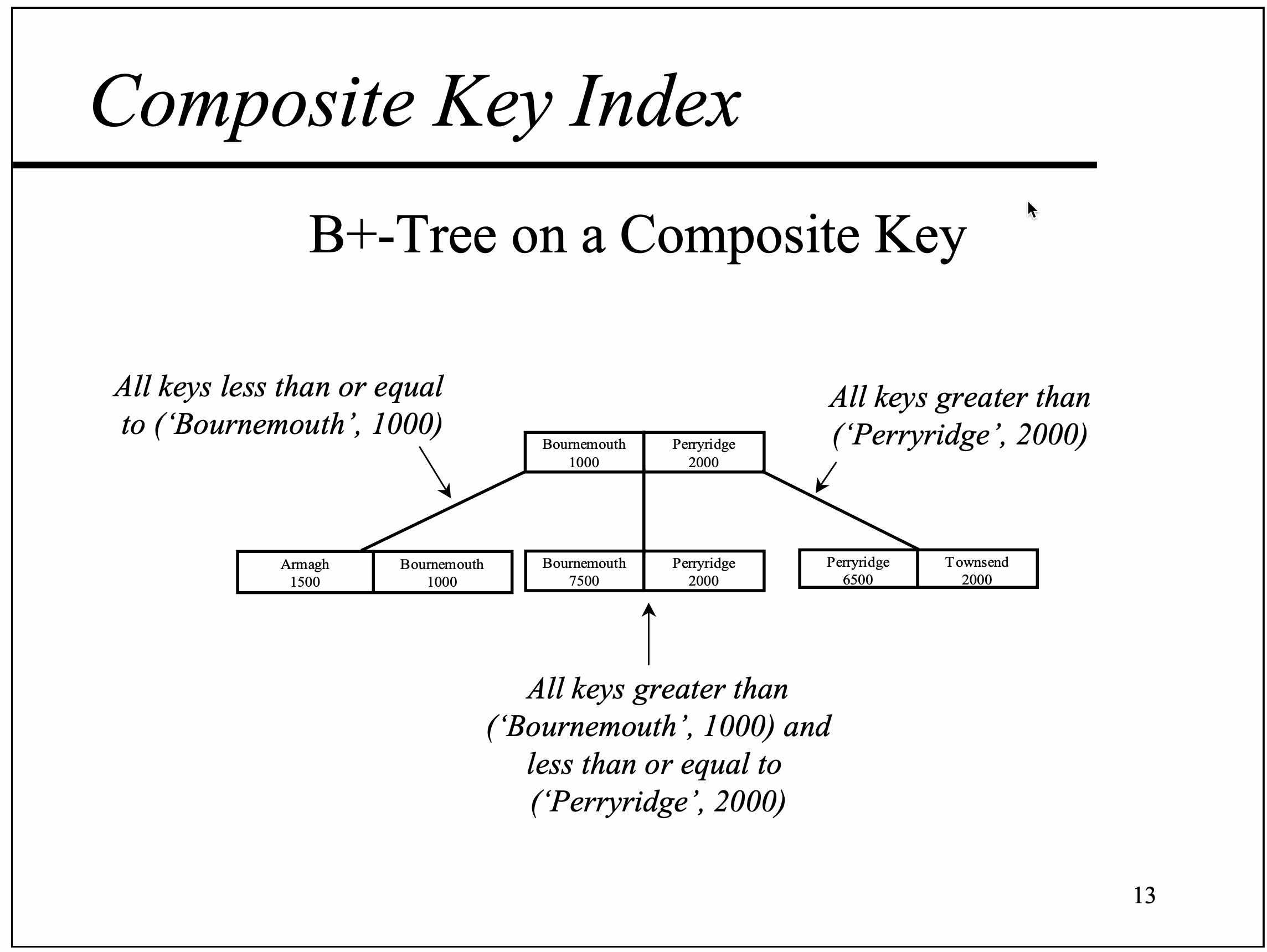
复合索引的B+树上的键值，就像单key的索引一样。和按字母顺序排列一个句子一样，复合索引中各个字段的顺序很重要。例如，下图为复合索引 (branch_name, balance) 的 B+树

1. 例如，(Bournemouth, 1000) 小于等于 (Bournemouth, 1000) ，因此它出现在第一个叶节点中； (Bournemouth, 7500) 大于 (Bournemouth, 1000) ，因此它出现在第二个叶节上

2. 例如，尽管 (Armagh, 1500) 第二个字段的值大于(Bournemouth, 1000)对应字段的值。字段的顺序意味着 (Bournemouth, 1000) 小于 (Bournemouth, 1000)

因此，上面的B+树可以用来搜索 (branch_name) 或 (branch_name, balance) ，而不能搜索 (balance)。例如，balance=2000 出现在B+树的两个路径中。

聚簇索引

由B+树的结构可知，数据记录本身被存于叶子节点上。就要求同一个叶子节点内（大小为一个内存页或磁盘页）的各条数据记录按主键顺序存放，因此每当有一条新的记录插入时，B+树会根据其主键将其插入适当的节点和位置

1. 如果使用递增的字段作为主键，新增记录就会添加到当前索引节点的后面。不需要因为插入移动已有数据，因此写入效率很高

2. 如果使用随机的字段作为主键，新增记录需要插入到索引的中间位置 。为了将新记录插到合适位置而移动已经存在的数据。同时频繁的移动、分页操作造成了大量的碎片，降低磁盘读写速度

总结

1. 为什么使用B+树，而不是B树作为底层数据结构？

   1. 树高较低，磁盘IO次数少
   2. 有利于范围、排序、分组等查询

2. 最左前缀匹配原则 为什么跟索引中字段顺序相关，而与查询中字段顺序无关？

   1. 因为索引中字段的顺序决定了建立一颗怎样的索引树
   2. 能否使用索引的本质在于，查询语句能否沿树游走

3. like 查询能够使用索引吗？

   1. 见 问题2
   2. % 开头的like语句无法沿树游走，因此无法使用索引

4. 主键为什么最好选择递增的字段？

   详见：聚簇索引

很多的知识都是串起来的，摸清了B+树，那么对于MySQL的 Explain工具 也就自然能够做到胸有成竹，基本的索引优化自然也就手到擒来。

参考

1. https://web.stanford.edu/class/cs346/2015/
2. https://pdfs.semanticscholar.org/0d7b/8b9172a69fa069c9c38b5f01bd37a498563c.pdf

本文作者 ： cyningsun
本文地址 ： https://www.cyningsun.com/08-25-2020/mysql-bplustree.html
版权声明 ：本博客所有文章除特别声明外，均采用 CC BY-NC-ND 3.0 CN 许可协议。转载请注明出处！